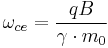Electron cyclotron resonance

Electron cyclotron resonance is a phenomenon observed both in plasma physics and condensed matter physics. An electron in a static and uniform magnetic field will move in a circle due to the Lorentz force. The circular motion may be superimposed with a uniform axial motion, resulting in a helix, or with a uniform motion perpendicular to the field, e.g., in the presence of an electrical or gravitational field, resulting in a cycloid. The angular frequency (ω = 2πf ) of this cyclotron motion for a given magnetic field strength B is given (in SI units)^[1] by

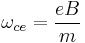$\omega_{ce}=\frac{eB}{m}$ .

where $e$ is the elementary charge and $m$ is the mass of the electron. For the commonly used microwave frequency 2.45 GHz and the bare electron charge and mass, the resonance condition is met when B = 875 G = 0.0875 T. For particles of charge q, rest mass m₀ moving at relativistic speeds v, the formula needs to be adjusted according to the special theory of relativity to:

$\omega_{ce}=\frac{qB}{\gamma\cdot m_0}$

where

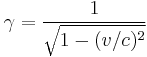$\gamma=\frac{1}{\sqrt{ 1 - (v/c)^2 }}$ .

1 In plasma physics
2 ECR ion sources
3 In condensed matter physics
4 References
5 See also

In plasma physics

An ionized plasma may be efficiently produced or heated by superimposing a static magnetic field and a high-frequency electromagnetic field at the electron cyclotron resonance frequency. In the toroidal magnetic fields used in magnetic fusion energy research, the magnetic field decreases with the major radius, so the location of the power deposition can be controlled within about a centimeter. Furthermore, the heating power can be rapidly modulated and is deposited directly into the electrons. These properties make electron cyclotron heating a very valuable research tool for energy transport studies. In addition to heating, electron cyclotron waves can be used to drive current. The inverse process of electron cyclotron emission can be used as a diagnostic of the radial electron temperature profile.

ECR ion sources

Since the early 1980s, following the award-winning pioneering work done by Dr. Richard Geller,^[2] Dr. Claude Lyneis, and Dr. H. Postma;^[3] respectively from French Atomic Energy Commission, Lawrence Berkeley National Laboratory and the Oak Ridge National Laboratory, the use of electron cyclotron resonance for efficient plasma generation, especially to obtain large numbers of multiply charged ions, has acquired a unique importance in various technological fields. Many diverse activities depend on electron cyclotron resonance technology, including

advanced cancer treatment, where ECR ion sources are crucial for proton therapy,
advanced semiconductor manufacturing, especially for high density DRAM memories, through plasma etching or other plasma processing technologies,
electric propulsion devices for spacecraft propulsion, where a broad range of devices (HiPEP, some ion thrusters, or electrodeless plasma thrusters),
for particle accelerators, on-line mass separation and radioactive ion charge breeding,^[4]
and, as a more mundane example, painting of plastic bumpers for cars.

The ECR ion source makes use of the electron cyclotron resonance to heat a plasma. Microwaves are injected into a volume, at the frequency corresponding to the electron cyclotron resonance defined by a magnetic field applied to a region inside the volume. The volume contains a low pressure gas. The microwaves heat free electrons in the gas which in turn collide with the atoms or molecules of the gas in the volume and cause ionization. The ions produced correspond to the gas type used. The gas may be pure, a compound gas, or can be a vapour of a solid or liquid material.

ECR ion sources are able to produce singly charged ions with high intensities (e.g. H⁺ and D⁺ ions of more than 100 mA (electrical) in DC mode^[5] using a 2.45 GHz ECR ion source).

For multiply charged ions, the ECR ion source has the advantage that it is able to confine the ions for long enough for multiple collisions to take place (leading to multiple ionization) and that the low gas pressure in the source avoids recombination. The VENUS ECR ion source at Lawrence Berkeley National Laboratory has produced in intensity of 0.25 mA (electrical) of Bi²⁹⁺.^[6]

Some of these industrial fields would not even exist without the use of this fundamental technology, which makes electron cyclotron resonance ion and plasma sources one of the enabling technologies of today's world.

In condensed matter physics

Within a solid the mass in the cyclotron frequency equation above is replaced with the effective mass tensor 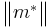$\begin{Vmatrix}m^*\end{Vmatrix}$ . Cyclotron resonance is therefore a useful technique to measure effective mass and Fermi surface cross-section in solids. In a sufficiently high magnetic field at low temperature in a relatively pure material

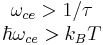
$\begin{matrix}\omega_{ce} > 1/\tau \\ \hbar \omega_{ce} > k_B T \\ \end{matrix}$

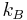where $\tau$ is the carrier scattering lifetime, $k_B$ is Boltzmann's constant and $T$ is temperature. When these conditions are satisfied, an electron will complete its cyclotron orbit without engaging in a collision, at which point it is said to be in a well-defined Landau level.

References

^ In SI units, the elementary charge e has the value 1.602×10^-19 coulombs, the mass of the electron m has the value 9.109×10^–31 kilograms, the magnetic field B is measured in teslas, and the angular frequency ω is measured in radians per second.
^ R. Geller, Peroc. 1st Int. Con. Ion Source, Saclay, p. 537, 1969
^ H. Postma, Phys. Lett. A, 31, p. 196, 1970
^ Handbook of Ion Source, B. Wolf, ISBN 0-8493-2502-1, p136-146
^ R. Gobin et al., Saclay High Intensity Light Ion Source Status The Euro. Particle Accelerator Conf. 2002, Paris, France, June 2002, p1712
^ VENUS reveals the future of heavy-ion sources CERN Courier, 6 May 2005

Electron cyclotron resonance

Contents

In plasma physics

ECR ion sources

In condensed matter physics

References

See also